Pre Calculus Portfolio:
Meadows or Malls: Report, Writeup, and Reflection
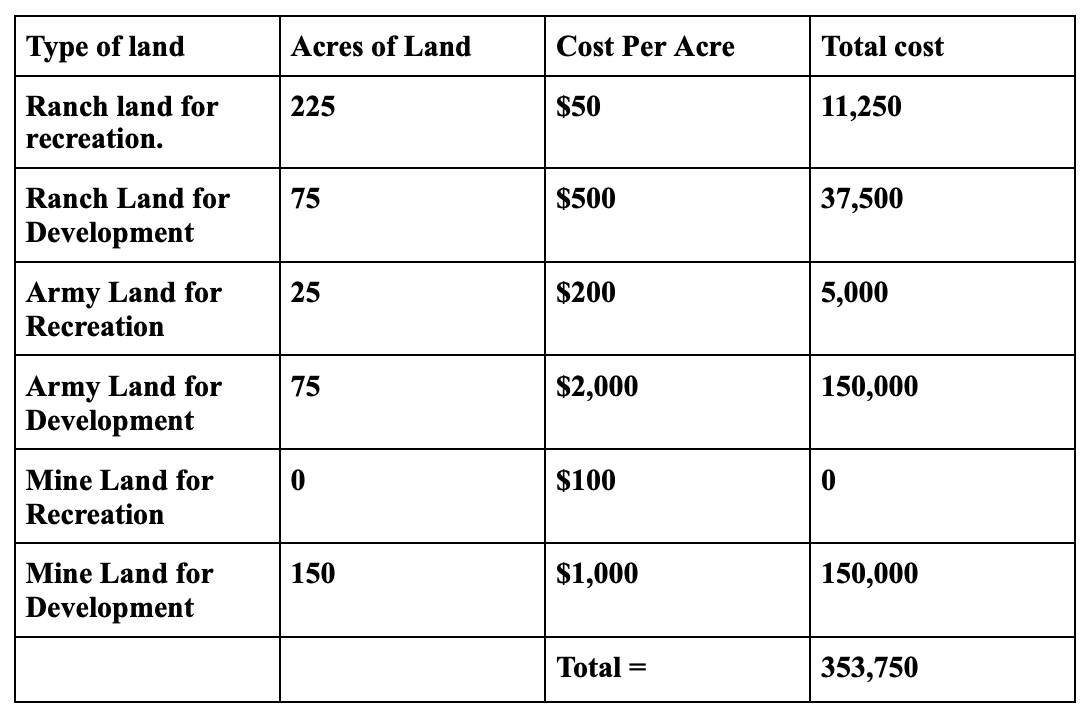
The Report
(Jack, Shaw, Adrian, Eli)
There is 550 acres of land that can be developed or used for recreation. The land comes from a mine, a ranch, and army land. The amount of acres for recreation is 250 acres and the amount for development is 300. The total cost for the land is 353,750.
The minimum amount of land to develop is 300 acres so we chose to stick with the minimum to lower the cost. We are using the most of the cheap land minimise the cost. Because there was one group of people that wanted most of the land for development and the other group wanted most of the land for recreation we chose to split up the land as equally as we could.
The Writeup
(individual, 1 page minimum, 4 points)
During this unit we went off in a lot of different directions to learn new ideas to eventually apply them to our unit problem. In order to find the best possible solution for the malls and meadows we first had to be able to understand what we needed to find. We needed to figure out what the cheapest way was to split up the land and also satisfy the 6 constraints.
2 = Ar + Ad = 100
3 = Mr + Md = 150
6 = Ar + Rd = 100
4 = Rd +Ad + Md + 300
9 = Mr0
In the start of the unit we worked on solving equations with 2 or more variables. This was a very valuable skill for the unit problem because solving this equation is like finding a variable and we ended up having a 6 variable equation in the end. The constraints are like boundaries for the equation. We also learned about independent and dependent variables when you are graphing because if an equation is dependent it has many solutions so their is not just one solution. When you are working with an independent equation it only has one solution meaning you can come to an answer. This helped figure out which constraints to use and if our problem was feasible. Another sill we learned was finding all corner points. This helps us because in our final problem it shows us what our most expansive choice could be. These are extremes and can help you find a general area for your solution. Leaning this was cool because all corner points are just the lines intersecting to create a point. Then we learned about 3D planes. Three Dimensional planes are planes that have an x,y, and z axis. This allows for you to create a 3D shape using a graph. This skill helps us find the answer to the final problem by allowing us to combine three different pieces of information to get an exact point. The Final skill we learned was Matrices. Matrices are a way to do linear equations with many numbers. These were very confusing but once you get a hang of them they make a lot of sense. Using matrices we were able to find the most feasible solution by calculating our variables. In the end we had to do so many different matrices that I got very lost but in the end it made sense because each new matrice was a different variable.
The Reflection
(individual, 2 paragraphs minimum, 2 points)
Throughout this unit I definitely struggled a lot. I would be taught a new subject and asked to do it and would be completely lost. I had a really hard time starting most of their new subjects because I didn't know where to start. It took alot of perseverance and frustration until I could understand the subject. I would tell myself to do at least one problem then after that it would get easier because I could apply my process from the first question to the others.
One thing from this unit that really helped me was when we went back to school. Even though they were just half day it really helped me to be in class doing the work with my peers and collaborating with them. It also helped me to be able to have the teacher explain the work directly and be able to answer questions instantly.When I am at home I tend to have a bad habit of putting off work for later that night and when I get to it I forget the lesson that we had earlier that day. Being back in school has helped me alot. I can talk to other students about the work and the imper learning is a lot easier to understand than being online.
(Jack, Shaw, Adrian, Eli)
There is 550 acres of land that can be developed or used for recreation. The land comes from a mine, a ranch, and army land. The amount of acres for recreation is 250 acres and the amount for development is 300. The total cost for the land is 353,750.
The minimum amount of land to develop is 300 acres so we chose to stick with the minimum to lower the cost. We are using the most of the cheap land minimise the cost. Because there was one group of people that wanted most of the land for development and the other group wanted most of the land for recreation we chose to split up the land as equally as we could.
The Writeup
(individual, 1 page minimum, 4 points)
During this unit we went off in a lot of different directions to learn new ideas to eventually apply them to our unit problem. In order to find the best possible solution for the malls and meadows we first had to be able to understand what we needed to find. We needed to figure out what the cheapest way was to split up the land and also satisfy the 6 constraints.
- RR is the number of acres of ranch land to be used for recreation
- AR is the number of acres of army land to be used for recreation
- MR is the number of acres of mining land to be used for recreation
- RD is the number of acres of ranch land to be used for development
- AD is the number of acres of army land to be used for development
- MD is the number of acres of mining land to be used for development
2 = Ar + Ad = 100
3 = Mr + Md = 150
6 = Ar + Rd = 100
4 = Rd +Ad + Md + 300
9 = Mr0
In the start of the unit we worked on solving equations with 2 or more variables. This was a very valuable skill for the unit problem because solving this equation is like finding a variable and we ended up having a 6 variable equation in the end. The constraints are like boundaries for the equation. We also learned about independent and dependent variables when you are graphing because if an equation is dependent it has many solutions so their is not just one solution. When you are working with an independent equation it only has one solution meaning you can come to an answer. This helped figure out which constraints to use and if our problem was feasible. Another sill we learned was finding all corner points. This helps us because in our final problem it shows us what our most expansive choice could be. These are extremes and can help you find a general area for your solution. Leaning this was cool because all corner points are just the lines intersecting to create a point. Then we learned about 3D planes. Three Dimensional planes are planes that have an x,y, and z axis. This allows for you to create a 3D shape using a graph. This skill helps us find the answer to the final problem by allowing us to combine three different pieces of information to get an exact point. The Final skill we learned was Matrices. Matrices are a way to do linear equations with many numbers. These were very confusing but once you get a hang of them they make a lot of sense. Using matrices we were able to find the most feasible solution by calculating our variables. In the end we had to do so many different matrices that I got very lost but in the end it made sense because each new matrice was a different variable.
The Reflection
(individual, 2 paragraphs minimum, 2 points)
Throughout this unit I definitely struggled a lot. I would be taught a new subject and asked to do it and would be completely lost. I had a really hard time starting most of their new subjects because I didn't know where to start. It took alot of perseverance and frustration until I could understand the subject. I would tell myself to do at least one problem then after that it would get easier because I could apply my process from the first question to the others.
One thing from this unit that really helped me was when we went back to school. Even though they were just half day it really helped me to be in class doing the work with my peers and collaborating with them. It also helped me to be able to have the teacher explain the work directly and be able to answer questions instantly.When I am at home I tend to have a bad habit of putting off work for later that night and when I get to it I forget the lesson that we had earlier that day. Being back in school has helped me alot. I can talk to other students about the work and the imper learning is a lot easier to understand than being online.
Jack Tescher
Unit 1 Portfolio
12/1/20
The Orchard Hide Out:
Cover Letter:
In the Orchard Hideout unit, we covered a lot of information. From the distance from a point to a point to the Pythagorean theorem when you are talking about the area of a circle. When we were starting this unit we worked on the distance from a point to a line and then when we had fully covered that we started to work on the best fit line or last line of sight. These directly correlate because how you prove that a line is the best fit is by proving the distance from that line to a point is the greatest out of all the possibilities that the line could be. I found that all the work that we did this unity was slowly building us up to because to answer the unit question.
Top start to find the unit question I need to first understand The Pythagorean theorem and Coordinate Geometry. One of the pieces of work we did this year that represents The Pythagorean Theorem and Coordinate Geometry is the In Or Out hand out that involved us trying to find if a point was inside our outside of a coordinate plane of 10. You had to be able to understand coordinate plains to complete this handout without having to completely write out every point. When I complete this assignment I had to ask myself first if the x or y coordinate was over 10 and then if it was then I would ask if it was close to the edge it could be off of the coordinate plane because of the curvature of the orchard. Using this technic answered most of the problems but for a few of them, I had to see if the math checked out by using the Pythagorean theorem using the coordinate Y value as the A value and the X value as the B. Then doing A^2 + B^2 to find C^2 and doing the square root of that number to find the distance from the center to the coordinate point.
The other key concepts that we had to learn before I could answer the unit problem Circles and the square-cube law. These concepts were a bit easier for me to understand because they are concepts that are more easily visualized. The handout I chose for these concepts is the Square cube law because when I did this assignment it made the concept clear when I wasn’t getting it before. The square-cube law is when you increase the size of a shape and have to find the volume and area. To find the volume of the different sized shapes you must scale with the square of the length and when you are finding the volumearea of the new shape you have to scale with the cube of the length.
The hardest part about this unit for me was the proof because most of the time I know how to complete the math concept I just have troupe proving why my answer is correct and show how I got there. Having this burden of always proving our answers was annoying to do at the moment but because able to back yourself up completely even in a subject like math. Having practice proving our work in this unit I feel I am much more efficient at proving my work.
Unit Problem:
The Unit question Is “How soon after they planted the orchard would the center of the lot become a true “orchard hideout”?” How you first have to answer this question is by understanding the orchard as a coordinate plane and what the last line of the sign is. The last line of sight is a line that is drawn from the center of a coordinate plane and is the farthest away from any point. How you find that distance to prove that your line is the last line of sight. How you do this is by finding the distance from the cent to the point that is farthest out in the orchard but also closest to your line. This can be shown here. Then using the Pythagorean theorem and the square-cube law will help you find that distance from the last line of sight and the trees that close to that line. How you do this is by looking at the orchard as a coordinate plane and drawing a right triangle with the most acute side at the center and the right-angled side near the edge of the orchard. Shown below. After you have found this triangle and used the Pythagorean theorem to ding the lengths of all its sides you can use the square-cube law to scale down the triangle until the scaled downs triangle's side A is equidistant from the last line of sight to the tree its closest to. For the orchard hideout, this distance would be 2.4 inches. Next using the distance from the point to the line or how much the radius of the tree must grow to block out the line of sight you can find the area of the tree when it is the largest it needs to be. Using pie and the area of a circle equation you can find the area of the tree when it is blocking the line of sight then subtract the area of the tree when it is starting. Finally, you will divide the area of the new tree by 1.5 because that is the amount to which the area grows every year. The answer I came to is 11.7 years. All the math I did for this equation is on this document.
Selection Of Work:
Reflection:
The math concepts in this unit for me were mostly easy because they made sense to me and I could do the problems I just had trouble with coming up with proof and an explanation for my answers. I have never done this rigorous proof in math. When I would struggle with coming up with proof I would get very frustrated because I had already completed the math and got the correct answer it felt like coming up with proof was pointless. But as we got deeper and deeper into this unit I started to get better at coming up with the proof for the problems but also was able to see the benefit of being able to come up with proof. If you have a proof for something then no one can tell you that you are wrong because you have evidence to back up your claim.
Even though I still have trouble coming up with proof and it can still be frustrating I can see how this will benefit me in not only future math classes but in all my classes and any time I have to back myself up. Have to create so much proof has made me think about how important it is especially in this day n age with how much fake or false information is shown to us. It makes me want to have more fact-checking in the work especially in the media. Too many media sources with thousands of followers will deliver them false information to sway them in a certain way and it does not allow people to look at the data that is real and then create their own opinions on it. People are also having ideas just be implemented in their brain without having to think “Is this real or are they lying?” You shouldn't have to ask yourself this question when you're watching a news channel or any kind of media is delivering you news or information and that is why we need to have more proof when we make claims.
Unit 1 Portfolio
12/1/20
The Orchard Hide Out:
Cover Letter:
In the Orchard Hideout unit, we covered a lot of information. From the distance from a point to a point to the Pythagorean theorem when you are talking about the area of a circle. When we were starting this unit we worked on the distance from a point to a line and then when we had fully covered that we started to work on the best fit line or last line of sight. These directly correlate because how you prove that a line is the best fit is by proving the distance from that line to a point is the greatest out of all the possibilities that the line could be. I found that all the work that we did this unity was slowly building us up to because to answer the unit question.
Top start to find the unit question I need to first understand The Pythagorean theorem and Coordinate Geometry. One of the pieces of work we did this year that represents The Pythagorean Theorem and Coordinate Geometry is the In Or Out hand out that involved us trying to find if a point was inside our outside of a coordinate plane of 10. You had to be able to understand coordinate plains to complete this handout without having to completely write out every point. When I complete this assignment I had to ask myself first if the x or y coordinate was over 10 and then if it was then I would ask if it was close to the edge it could be off of the coordinate plane because of the curvature of the orchard. Using this technic answered most of the problems but for a few of them, I had to see if the math checked out by using the Pythagorean theorem using the coordinate Y value as the A value and the X value as the B. Then doing A^2 + B^2 to find C^2 and doing the square root of that number to find the distance from the center to the coordinate point.
The other key concepts that we had to learn before I could answer the unit problem Circles and the square-cube law. These concepts were a bit easier for me to understand because they are concepts that are more easily visualized. The handout I chose for these concepts is the Square cube law because when I did this assignment it made the concept clear when I wasn’t getting it before. The square-cube law is when you increase the size of a shape and have to find the volume and area. To find the volume of the different sized shapes you must scale with the square of the length and when you are finding the volumearea of the new shape you have to scale with the cube of the length.
The hardest part about this unit for me was the proof because most of the time I know how to complete the math concept I just have troupe proving why my answer is correct and show how I got there. Having this burden of always proving our answers was annoying to do at the moment but because able to back yourself up completely even in a subject like math. Having practice proving our work in this unit I feel I am much more efficient at proving my work.
Unit Problem:
The Unit question Is “How soon after they planted the orchard would the center of the lot become a true “orchard hideout”?” How you first have to answer this question is by understanding the orchard as a coordinate plane and what the last line of the sign is. The last line of sight is a line that is drawn from the center of a coordinate plane and is the farthest away from any point. How you find that distance to prove that your line is the last line of sight. How you do this is by finding the distance from the cent to the point that is farthest out in the orchard but also closest to your line. This can be shown here. Then using the Pythagorean theorem and the square-cube law will help you find that distance from the last line of sight and the trees that close to that line. How you do this is by looking at the orchard as a coordinate plane and drawing a right triangle with the most acute side at the center and the right-angled side near the edge of the orchard. Shown below. After you have found this triangle and used the Pythagorean theorem to ding the lengths of all its sides you can use the square-cube law to scale down the triangle until the scaled downs triangle's side A is equidistant from the last line of sight to the tree its closest to. For the orchard hideout, this distance would be 2.4 inches. Next using the distance from the point to the line or how much the radius of the tree must grow to block out the line of sight you can find the area of the tree when it is the largest it needs to be. Using pie and the area of a circle equation you can find the area of the tree when it is blocking the line of sight then subtract the area of the tree when it is starting. Finally, you will divide the area of the new tree by 1.5 because that is the amount to which the area grows every year. The answer I came to is 11.7 years. All the math I did for this equation is on this document.
Selection Of Work:
Reflection:
The math concepts in this unit for me were mostly easy because they made sense to me and I could do the problems I just had trouble with coming up with proof and an explanation for my answers. I have never done this rigorous proof in math. When I would struggle with coming up with proof I would get very frustrated because I had already completed the math and got the correct answer it felt like coming up with proof was pointless. But as we got deeper and deeper into this unit I started to get better at coming up with the proof for the problems but also was able to see the benefit of being able to come up with proof. If you have a proof for something then no one can tell you that you are wrong because you have evidence to back up your claim.
Even though I still have trouble coming up with proof and it can still be frustrating I can see how this will benefit me in not only future math classes but in all my classes and any time I have to back myself up. Have to create so much proof has made me think about how important it is especially in this day n age with how much fake or false information is shown to us. It makes me want to have more fact-checking in the work especially in the media. Too many media sources with thousands of followers will deliver them false information to sway them in a certain way and it does not allow people to look at the data that is real and then create their own opinions on it. People are also having ideas just be implemented in their brain without having to think “Is this real or are they lying?” You shouldn't have to ask yourself this question when you're watching a news channel or any kind of media is delivering you news or information and that is why we need to have more proof when we make claims.
